Platonic Solids
I was the first to consider Coxeter (reflection) groups in the Clifford framework, which affords a uniquely simple prescription for reflections. Via the Cartan- Dieudonné theorem, performing two reflections successively generates a rotation, which in Clifford algebra is described by a spinor that is simply the geometric product of the two vectors generating the reflections. I have shown that in such a geometric setup, the widely used quaternionic representations of rank-3 and rank-4 Coxeter groups actually have very nice geometric interpretations. It has been overlooked that the rank-3 representations in terms of pure quaternions are simply the Hodge duals of the root vectors and that the quaternionic rank-4 representations are the 3D spinors generated by the 3D reflections. This approach yields a very simple construction of the binary polyhedral groups, and with my result the versor formalism in fact allows for the first time a unified treatment of the chiral, full and binary groups in the same framework. These groups are currently very attractive for model building in neutrino and flavour physics, and a unified and streamlined treatment could therefore open up new directions in these fields.
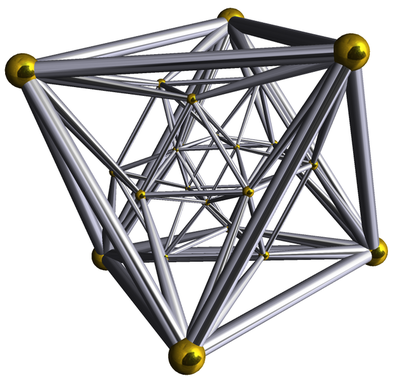
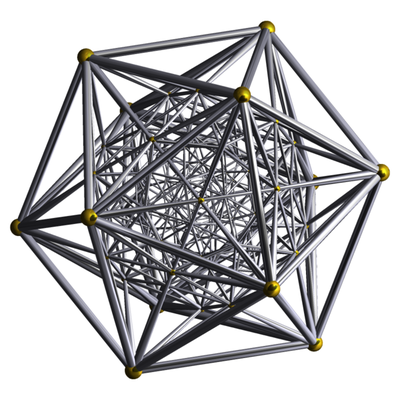
The above Clifford spinors have a natural 4D Euclidean structure and can thus be interpreted as 4D vectors. I have considered the root systems of the 3D Coxeter groups that describe the symmetries of the Platonic solids in this Clifford algebra approach. I have shown that the corresponding 3D spinors, when reinterpreted as 4D vectors, are the 4D analogues of the Platonic solids (e.g. the 16-cell, the 24-cell and the 600-cell). In fact, a similar construction for the prisms given by A1 ⊕ I2(n) yields the 4D polytopes described by I2(n) ⊕ I2(n). Thus, the 3D spinorial view establishes a previously unknown link by generating the 4D polytopes from the 3D polytopes. Furthermore, this explains compellingly for the first time certain otherwise mysterious symmetries of these polytopes, that are rather more obvious when expressed as 3D spinors. In fact, these polytopes are all root systems, thereby themselves generating Coxeter groups of rank 4.
The above Clifford spinors have a natural 4D Euclidean structure and can thus be interpreted as 4D vectors. I have considered the root systems of the 3D Coxeter groups that describe the symmetries of the Platonic solids in this Clifford algebra approach. I have shown that the corresponding 3D spinors, when reinterpreted as 4D vectors, are the 4D analogues of the Platonic solids (e.g. the 16-cell, the 24-cell and the 600-cell). In fact, a similar construction for the prisms given by A1 ⊕ I2(n) yields the 4D polytopes described by I2(n) ⊕ I2(n). Thus, the 3D spinorial view establishes a previously unknown link by generating the 4D polytopes from the 3D polytopes. Furthermore, this explains compellingly for the first time certain otherwise mysterious symmetries of these polytopes, that are rather more obvious when expressed as 3D spinors. In fact, these polytopes are all root systems, thereby themselves generating Coxeter groups of rank 4.
|
iIn fact, I have shown more generally that any 3D root system induces a 4D root system in this way, explaining the exceptional structures D4, F4 and H4 in terms of three-dimensional geometry alone (induced from A3, B3 and H3). I have given H4 a geometric meaning as spinors in the Clifford algebra of 3D, with tantalising possibilities for the closely related group E8. In the corresponding case in 2D, I have shown that the infinite family of root systems I_2(n) is self-dual under the Clifford spinor construction.
More recently, I have constructed the E8 root system from the icosahedron, and have found a web of ADE correspondences connecting 3D geometry, 4D geometry and higher-dimensional geometries. |