Mathematical Virology
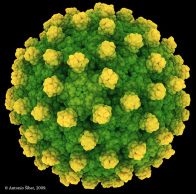
Viruses are perhaps the most mysterious and intriguing biological entities. Where biology usually dazzles with its manifold complexity and flexibility, viruses impress with their minimalism, existing at the boundary between living organisms and inanimate macromolecules. Whilst the largest viruses are larger and more complex than the smallest bacteria, the smallest viruses have only very few genes. This genetic economy, however, does not mean that viruses are not highly complex and adapted, with most viral components performing several different functions. For instance, Hepatitis B virus has only 4 genes, only one of which encodes the structure of the virus.

Many viruses therefore use the same structural building blocks and take advantage of symmetry; if one can make a square, one can assemble 6 copies into a cubic container. The largest such symmetry available arises by assembling 20 triangles into an icosahedron (20-sided dice) and many viruses have this shape. The strongest constraints on virus structure therefore come from geometry rather than biochemistry. Similar symmetry principles apply in many other areas of the natural world, such as football-shaped cages consisting of carbon atoms (fullerenes), salt crystals etc.
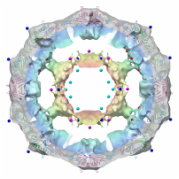
However, viruses might be even more economical by not only applying symmetry to its two-dimensional surface triangles, but instead to its entire three-dimensional structure. Reidun Twarock's group in York has pioneered this idea of `affine symmetry', which has allowed to predict the inner structure of a virus (the distribution of nucleic acid) from its outer container (capsid).
